Instructor
Dr. Julie Bracken
Preparation
I bought the text a few weeks before the start of the term and told myself that I would get a head start on the reading, but I only made it through the first chapter.
A better preparation was linear algebra, which I took last semester. This course introduced me to the concepts of identity, surjectivity, and injectivity, expanded my understanding of an inverse, and offered a good review of domains, codomains, and ranges. All of these ideas came up again and again in group theory, so I’m glad I’d seen them before.
Text
The course followed chapters two through sixteen of A Book of Abstract Algebra by Charles Pinter. I quite liked this book. It’s small, like a novel, and so easy to carry around. The chapters are short, some only a few pages, which is nice because I often find myself having to reread a section once or twice before I start to understand. Knowing that I only have to go back a few pages makes this a much easier pill to swallow.
My favorite part of the book, though, is that it has a voice. Imagine that, math with a voice.
I’m taking ring and field theory next term, which will follow the second half of the book. I’m looking forward to finishing it.
Lectures
The class periods for this class were very different than what I’d experienced over the past year at Portland Community College, where I’d taken Calculus III and IV and Linear Algebra. There were no handouts, no worksheets, no group work, no opportunities to try out a problem on one’s own. Dr. Bracken simply went through the material and then paused for questions. It was like a traditional lecture with the addition of being able to ask questions.
Some of my notes. I take a lot of pride in how my notes come together. MUJI notebook, Marvy LePen pens.
Dr. Bracken’s handwriting is clear and she would alternate between opposing sides of the whiteboard so that you we had a chance to get everything down before it was erased. And it was a good thing, too, because she moved fast. There was many a class period wherein I felt like I was writing as quickly as I could for the entire period. And if I hadn’t done the reading beforehand, I’d often finish the period without any idea what I’d just listened to.
All of that said, she did pause to ask if anyone had any questions after pretty much every proof and example. The problem was that I’d sometimes end up so lost at the end of the example that I wouldn’t even know what question to ask besides, “Can you explain that one more time?”
Strategy
There were a few things that I think helped me succeed in this class, and then another that regret not doing more of.
Start early
My plan was to always start on work as soon as possible. Sometimes I was successful, and sometimes I wasn’t. I generally had the homework done a week before it was actually due. And while I did my best to stay ahead on the reading, sometimes I wouldn’t get to it until after its corresponding lecture. As I mentioned above, if I hadn’t done the reading beforehand the lectures were very difficult to follow.
Make flashcards
Another thing I tried to keep up on was making flashcards (here’s the deck I created over the course of the term). I use the spaced-repetition application Anki on my computer and my phone and have found it to be a critical part of my learning strategy, whether I’m studying math or computer science or foreign languages.
Ideally I’d be making new flashcards after each class period (a feat I achieved when I took linear algebra last term), but for this course I just made them in preparation for the two midterms and the final. This seemed to work well enough, but I’ll certainly try to make it more of a regular habit for my math classes next term.
The easy part with flashcards is the reviewing. I tried to do this every day (except weekends, which I typically treat as a schoolwork sabbath). Depending on how many cards I had to review, it usually took about ten or fifteen minutes. Not bad.
Ask questions
One thing I wish that I’d done more was to attend office hours. I actually only went once, when I was preparing for the final exam. In lieu of office hours, I emailed questions, a lot of questions. I must’ve emailed the instructor 30 times over the course of the term, if not more. This was largely because I didn’t know where the holes in my understanding were until I attempted the problems and proofs myself. Incidentally, this is also one of the benefits of using LaTeX for homework: when emailing questions I can simply copy and paste or screenshot my work and email it along. No need to type up what I’d already written by hand or scan anything in.
Still, office hours would’ve been easier. Plus, there’s the idea that the person doing the talking is the person doing the learning. Without much opportunity to talk through my understanding in class, office hours would be the next best thing. I’m not sure when the office hours for my classes next term will be, but assuming it’s possible I’m planning on putting them on my schedule and attending as a matter of course.
Assignments
There were five assignments, each of which were made up of about half a dozen problems pulled from the text. With a few exceptions, the problems were proofs. Here are a few examples:
- Let a and b each be equal to its own inverse. Prove that ba is the inverse of ab.
- G is a group, a ∈ G, and f : G → G is defined by f(x)=ax. Determine whether f is injective or surjective or both.
- Prove that if x² ∈ H for every x ∈ G, then every element of G/H is its own inverse. And conversely, that if every element of G/H is its own inverse, then x² ∈ H for all x ∈ G.
I usually spent twenty minutes to an hour on the average question. Whenever possible, I tried to look at a problem before taking breaks or quitting for the day so that my subconscious would have a chance to mull it over. As I do with all of my math assignments, I typed these up using LaTeX and Overleaf.
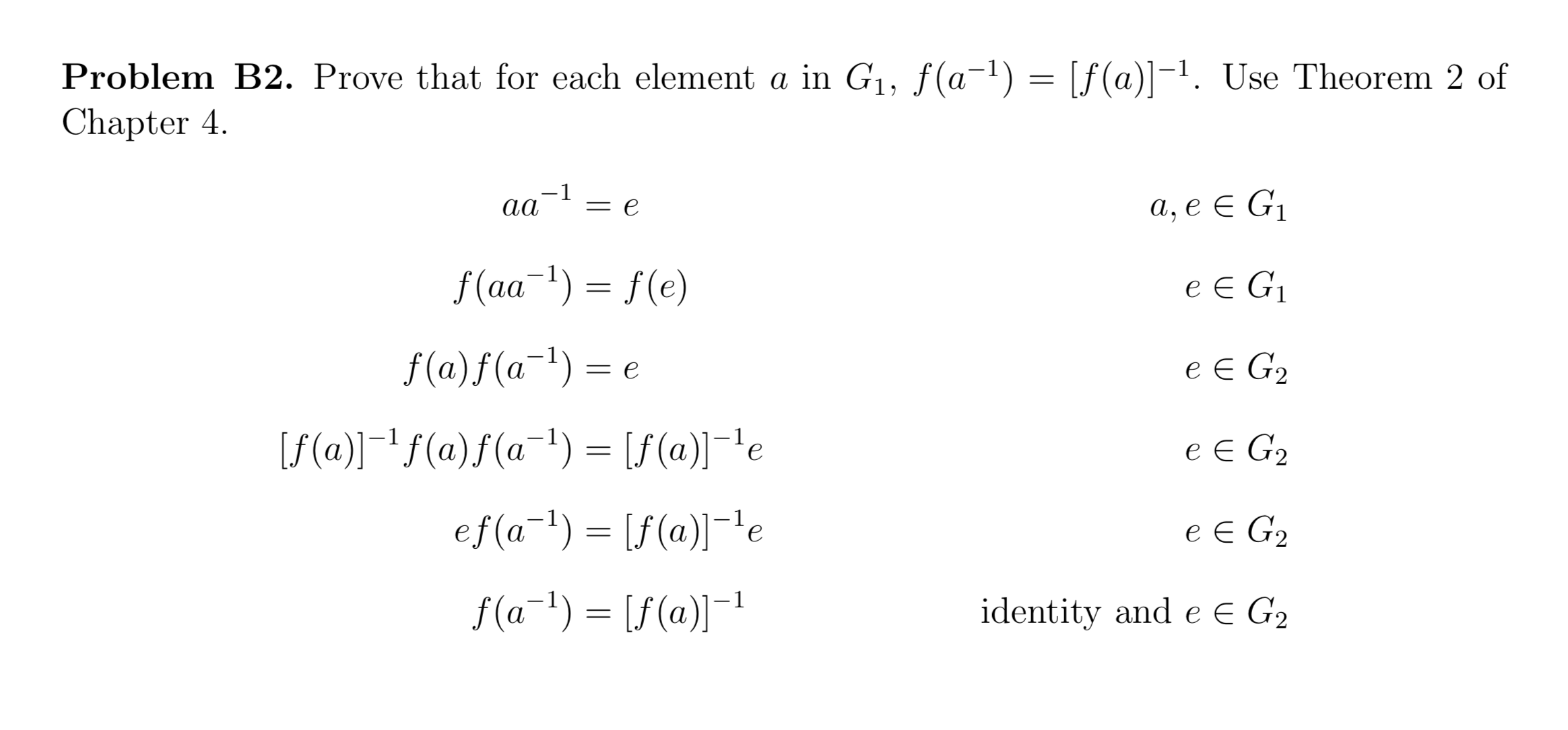LaTeX can be a pain to write but the result is gorgeous.
It takes more time than writing them out by hand, but I think the end result (which is gorgeous) is worth the effort.
Exams
There were three exams: two midterms and a final. Each covered about a third of the course. Each was comprised of four or five questions, most of which were similar to the homework problems described above.
I found all the exams very difficult. No matter how much I studied, I still found that I had to really puzzle over the questions. Thankfully, Dr. Bracken provided practice questions which I used as my primary source of study material. She gave these out a week or so before each exam, which meant that I had enough time to do a few problems each day until I’d done all of them two, three, or four times.
I received a 95 percent on the first exam, a 75 percent on the second, and a 91 percent on the third. I studied about the same amount for each, though I made a fatal error on the second. For one of the questions I assumed something I was actually trying to prove, which meant that I lost almost all the points available for the question. And since there were only three other questions, it meant that that one mistake took a large chunk out of my final score.
I had to include one more LaTeX screenshot to distract myself from the pain of the midterm I got 75 percent on.
The hardest part about the exams, I think, was lacking the ability to check my work. When I was taking calculus and linear algebra, I was always keen to figure out ways to work problems backwards, or at least do a general sniff test to ensure that my answer was on the right track. I’ve yet to figure out those methods for group theory proofs. Maybe there aren’t any.
Resources
As with all of my math classes, I found the Mathematics Stack Exchange to be a lot of help. I only ended up posing one question of my own, but I read through countless questions posted by others.
Difficulty and Time Commitment
This was the most conceptually challenging course I’ve ever taken in any subject. I have never felt more dumb in a class, nor have I ever felt more satisfied once I started to grasp the material. This time between feeling dumb to satisfied often took a week or more for any particular topic, and so it was easy to lose faith.
At one point toward the end of the term a student asked Dr. Bracken how she’d come to know abstract algebra so well. “I’ve been doing this for thirteen years,” she said. “Think about the math you were doing thirteen years ago. You’ve come a long way from then, too.”
For my part, thirteen years ago I would’ve been a sophomore in my first round of college. I would’ve just recently dropped a trigonometry course to prevent myself from earning an F. It’d be another six or seven years before I’d take another math class. Needless to say, Dr. Bracken’s response stuck with me, and I expect that I’ll be coming back to it, both on my own and with my students, for years to come.
Now, back to group theory. I spent about 130 hours on the class over the course of the term, including three hours per week for lectures. This was in addition to the three other courses I took this term (capstone and a computer security course at Oregon State, and math history here at Portland State), plus all my non-school commitments (family, garden, reading, etc.).
What I Liked and What I’d Do Differently
I love it when an instructor designs a course with simplicity in mind. It’s clear that this was the case for this course:
- We only had one text, read sequentially.
- There were only five assignments, all of the same type.
- Point values were consistent between assignments and exams and added up to a nice even number.
- There were no other grading measures, like quizzes, projects, or participation.
Setting things up this way reduces the cognitive load associated with taking a class. It’s easy to keep track of what’s due and when, which allows more time and energy for focusing on what really matters: the material. All of that said, I think that this course may have pushed that idea too far. Here are a few things that I wish would’ve been different:
Working together
Group work can be a drag, but they offer students a chance to talk through their ideas - a critical means of learning. Not to mention the fact that they help students meet one another, which can be valuable for forming study groups and even just creating a sense of community in the classroom.
My turn, your turn
I wish that we’d had a chance to work through problems during class. As it was, I don’t remember a single instance over the course of the term in which the professor gave us a chance to work through a solution on our own. She paused regularly for students to call out answers and suggestions to her questions, but this isn’t the same thing as telling everyone to “take thirty seconds and figure this out for yourself.” This would’ve taken valuable class time, of course, but I think it’d be well-spent. And anyway, the fact that we finished the term with two full days for review tells me that we had a few minutes to spare.
Onward
As I’ve said, I found this course very difficult. And there were a few things that I wish were different. But I never found it frustrating or boring. Quite the opposite, in fact. I’m looking forward to continuing with the subject next term and hoping that the skills and strategies I’ve picked up this term will come in handy.