In addition to the two computer science courses I took at Oregon State this term, I also took Linear Algebra at Portland Community College. This post will serve as a short (or not so short) summary of what I learned, what I liked, and how I think the course could be improved.
Instructor
Marissa Major
Notes
The instructor prepared scaffolded notes which I used for almost all of my note-taking. By scaffolded, I mean that she had summarized the main points and introduced proofs and examples, and then we filled them out together. I think that this is an excellent way to structure lectures and notes.
From the student’s perspective, it’s valuable because you don’t risk copying down a critical point incorrectly or spending the entire lecture writing furiously (and not actually thinking about what you’re writing).
It’s probably more work for the instructor (I’ve never done it so I’m just imagining), but I’d think that the added benefit would be that it would force you to think through your lesson in detail before presenting it to students, rather than just thinking “OK, today I’ll cover x and use y and z as examples.”
Preparation
I didn’t do any formal preparation for this course, but as with many subjects in math, I was building on top of a previously-laid foundation. I’d covered vectors and n-dimensional space in Calculus IV, so none of that was particularly foreign, and I was familiar with several basic matrix operations (addition, multiplication, transpose) from another class I took this term in which we had to write a shell script which performed these operations.
Linear algebra becomes complicated quickly, but I don’t think that I would’ve done anything differently in terms of preparation. Perhaps if I’d had more time (and desire) to prepare, I would have watched the The Essence of Linear Algebra from 3Blue1Brown. This is a kind of birds-eye view of linear algebra and does an excellent job of developing visualizations and intuition for how matrices represent and modify geometric space.
Assignments
There were four types of assignments: in-class activities, regular homework, write-up homework, and a group presentation.
Regular Homework
We used WeBWork, which was OK. These assignments were due once a week and usually took me an hour or two to complete.
From an instructor’s perspective it’s probably advantageous to have homework automatically checked and graded, but I’m still partial to doing homework from the textbook with pencil and paper. The more I can get away from my computer (since it’s a fine-tuned distraction machine), the better.
Write-Up Homework
This was similar to the regular homework, except that we were to focus on presentation and clarity. Assignments were due every two or three weeks. They consisted of one or several problems to be completed in detail, such that anyone with a basic understanding of the subject matter could read through the solution and understand how the problem was solved.
I decided to complete these assignments using LaTeX, which I’d also used in my calculus courses in previous terms.
Using LaTeX was slow-going at first, but once I figured out the most common commands (how to use math mode, special characters, etc.) I found that it didn’t take me much longer to use LaTeX than to use pen and paper. And even if it did slow me down a bit, it was a positive change.
As I’ve written in other class review posts, learning takes time. Not time spent banging my head against the wall, but time to process and digest. Using a slightly slower method like LaTeX makes room for that passage of time so that I can really learn and understand the material. All of that said, my favorite part about using LaTeX is that the final product is just so damn pretty:
Two things that have helped me with LaTeX are having a good template (here’s one I found online) and a good online service for rendering and printing (I use Overleaf).
Group Presentation
We broke up into groups of four and gave a presentation on a particular application of linear algebra. There wasn’t a ton of application in the course, so I thought that this was an excellent way of showing what could be done with linear algebra. The topics were chosen for us. Some students presented on calculating the Fibonacci sequence with matrices, another group presented on cryptography. There were eight or ten topics in total.
My group presented on graph theory and adjacency matrices. An adjacency matrix is used to represent the relationship between nodes in graph theory. We zoomed in on two interesting aspects of this adjacency matrix.
First, if an adjacency matrix is raised to the kth power, then it will show the number of ways there are to travel from one node to another in k steps.
Second, the eigenvector corresponding to the dominant (largest) eigenvalue will show which nodes are the most “connected,” in terms of a concept called eigenvector centrality.
These were cool ideas, and I was happy to spend some time learning about them in detail, and then presenting my learning to the class. It also gave me an opportunity to learn how to use NumPy (to find matrix powers and eigenvectors), which I’d somehow put off until this point.
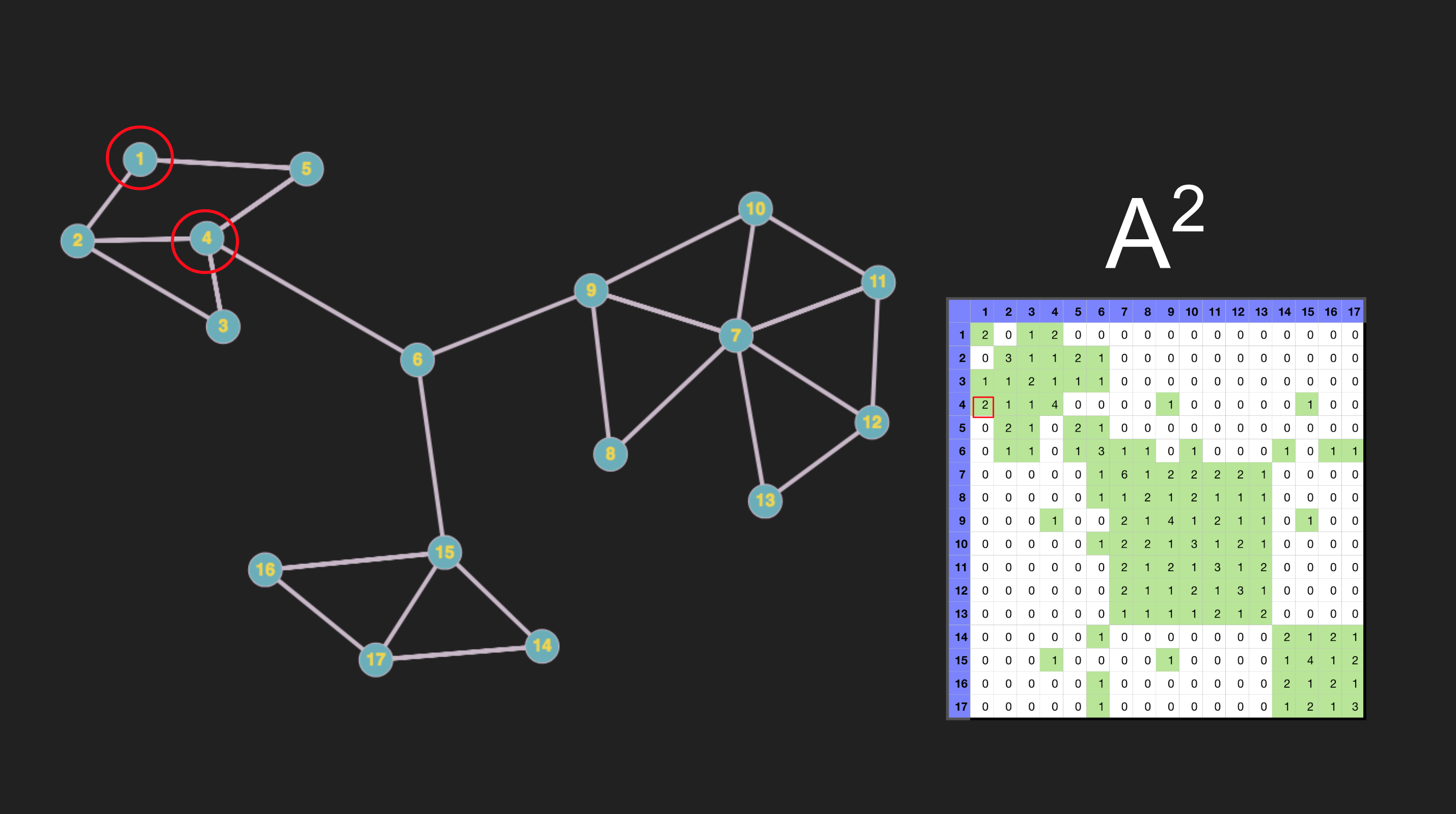One of the slides from our group presentation about graph theory and adjecency matrices.
In-Class Activities
These weren’t really formal assignments, but on a few occasions we were tasked with working with the other students at our table on a group of problems. I used to hate this style of work (since I’m shy by default), but now I’ve grown to like it. Not only does it force me to verbalize my thoughts and understanding (the one doing the talking is the one learning), but it also gave me a chance to get to know the people I sat with every week.
Exams
There was one midterm and one final. Beyond reviewing a few homework questions and keeping up with my flashcards (see below), I didn’t study much for the midterm. I even neglected to make a cheat sheet, which is something I almost always do when given the opportunity. So when I walked out of the classroom after taking it, I didn’t really know what to make of my performance. I figured I did OK, but not great. When I found out a few days later that I’d aced the midterm, I was very, very surprised. I definitely felt like I’d gotten a lucky break.
I didn’t want to push my luck for the final, so I spent a lot of time studying for it. I made a very detailed cheat sheet, studied flashcards for about fifteen minutes every day for the two weeks prior to the exam, and did a couple homework problems from every set that we’d been assigned.
When I finally took the final, I felt really good about it. There was one question that I asked for a hint on, but once I had the hint I felt confident that I was going the right direction.
I don’t think I’ll ever find out how I did (since the instructor never posted individual assignment or test grades online), but I couldn’t have done too poorly since I ended up with an A in the course.
Resources
- Anki: For flashcards
- RREF Calculator: When I wanted to save some time
- Another RREF Calculator: Slower, but shows intermediate steps
- Symbolab: For eigenvectors and other matrix math
- Linear Algebra on Khan Academy: Excellent videos from Sal Khan
- The Essence of Linear Algebra: Visualizations from 3Blue1Brown
- Overleaf: For LaTeX rendering and printing
Difficulty and Time Commitment
On the whole, this class was about as difficult as the calculus courses I’ve taken over the past few years. In linear algebra I found that the computational difficulty was relatively low, whereas the conceptual difficulty was relatively high. In my experience, this was the opposite of calculus, where the concepts are more straightforward but the computation of those concepts can be quite difficult.
My daughter was painting with watercolors and I wanted to keep busy, too. So I painted this interpretation of a matrix in row echelon form. Nerd alert!
I spent about 50 hours on this course, not including time in class. This time was spent completing regular and write-up homework, watching supplementary videos, and using flashcards. There are a ton of interrelated concepts in linear algebra, so I found that an app like Anki was a great way to keep them all straight. If you’d like to steal and build off of my Anki deck, you can download it here.
My other main commitments are my computer science classes at Oregon State (I took operating systems and software engineering this term) and my family.
What I Liked and What I’d Do Differently
There were a lot of things I liked about this course. First of all, the subject matter was fascinating. I loved that we were constantly generalizing relationships so that they were true for every vector, or every matrix, or every space no matter the number of dimensions, etc. It was similar to the mind explosion that accompanied the realization that x could stand in for a number. Incredible.
Another thing that I liked about linear algebra was learning about more and more modern math. This was also a cool part about calculus - knowing that what I was learning had only been a part of human understanding for a few hundred years (Newton was born in 1642, Leibniz in 1646). Linear algebra, for its part, is largely rooted in the middle of the 19th century.
I also loved the idea of matrices representing geometric transformations. Granted, the geometric manifestation of numbers and equations has been a part of basically every math class I’ve ever taken, but in linear algebra this idea really took off, especially as we were forced to think about spaces beyond two and three dimensions. This gets at the generalization idea I was talking about above.
As for the actual implementation of the course, I found it mostly enjoyable. Ms. Major was an engaging instructor. Her notes were good, the assignments and workload were reasonable, and she stressed conceptual understanding over computational perfection. On top of all of that, she had a good sense of humor, which is especially valuable in a math class.
That said, there were a few little things that bothered me. I felt like she missed several opportunities to make the class more manageable and enjoyable. It wasn’t uncommon to have homework due on a particular subject just a day after it was lectured on (I assume because the lectures got pushed back but the homework due dates stayed fixed). I felt like she didn’t have great awareness of which homework was due when, which could’ve alleviated this problem.
Another thing that I found annoying was that we were rarely allowed breaks over the course of the class period, especially since the periods lasted two hours and twenty minutes. Granted we’re adults and can leave the classroom when we want to, but the material is difficult and it’s easy to get lost. I’d rather not take the chance by missing five minutes of class. And hopefully it goes without saying, but taking brief mental breaks is critical when learning new things.
One more thing I would’ve done differently has to do with group project assignments. The way projects and groups were assigned was that we were randomly placed with three other students, and then we had to choose a topic as a group. I think a better way would’ve been to have students choose one or two topics they were interested in and then assemble the groups accordingly. A bit more work, sure, but I think it’d be worth the outcome.
Like I said, these are mostly small things. Except breaks - breaks are a big deal.