Whenever I finish a course in Oregon State’s computer science program, I write up a short (or not so short) blog post about what I learned and how I think the course can be improved. This serves three purposes: First, it helps guide students who’ve yet to take the course (or at least I hope it does). Second, it makes my learning visible. And third, it’s an exercise in thinking through how I would change a course if I were the one teaching it.
I doubt anyone will be looking to my site for tips on how to succeed in Calculus III or IV at Portland Community College, so I’m using this post as a meditation on how the two courses were taught and what lessons I’ve learned about teaching.
For the record, I took these two courses back to back: Calculus III (MTH 253) during winter term of 2018 and Calculus IV (MTH 254) in the spring.
Instructor
Noella Grady
Notes
The first thing about the courses that stuck out to me was that most of the notes had been prepared and printed in advance. The main ideas and formulas were included, as were lots of examples and problems. As the instructor lectured, it was the students’ responsibility to fill in the blanks. We’d work the problems and examples (following her direction), underline the important points, etc. Perhaps a better way to describe it is that she provided the scaffolding and it was our responsibility to fill in the details. Here’s an example of what I’m talking about:
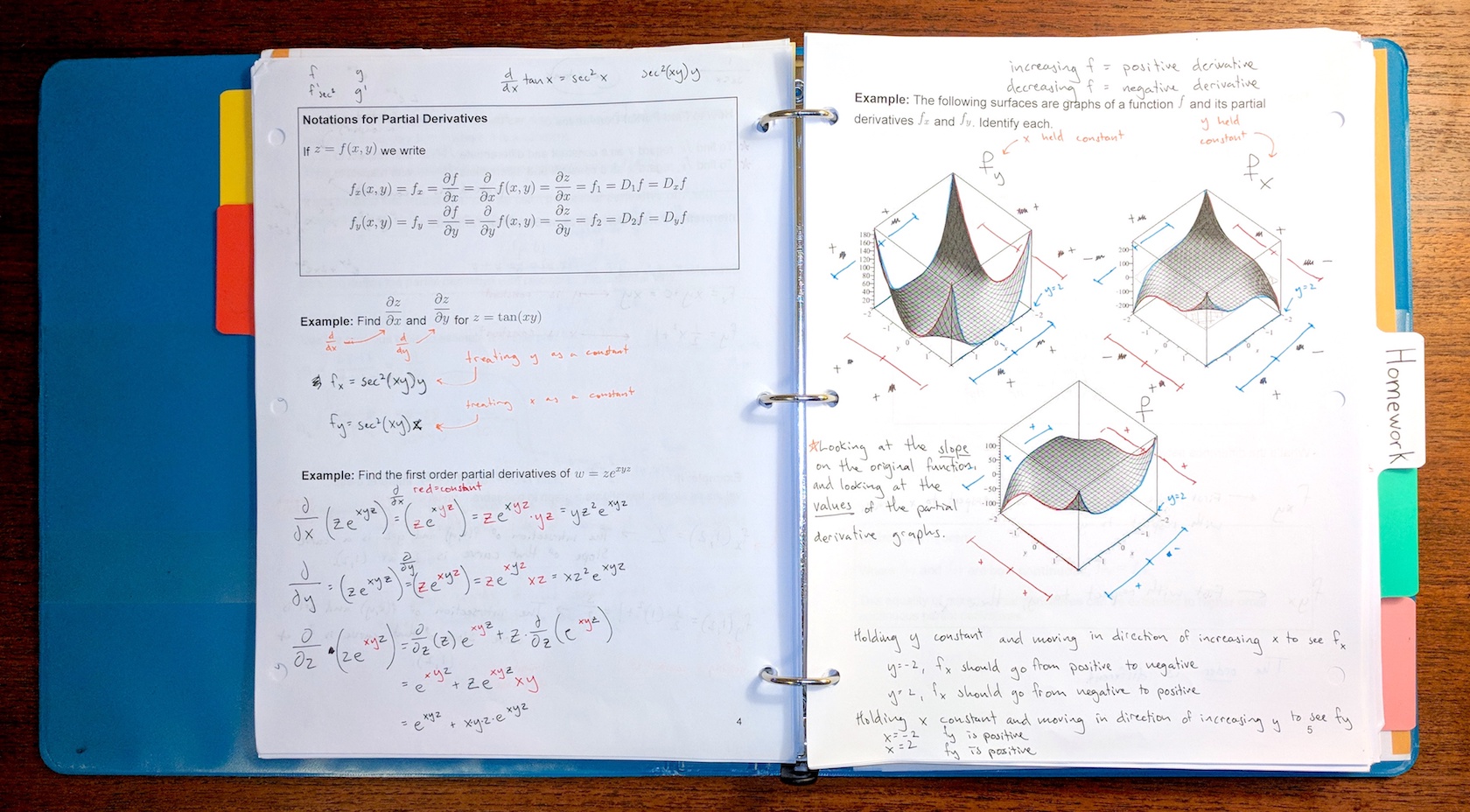 The printed parts were provided by the instructor. Everything in pen I added during the lecture.
The printed parts were provided by the instructor. Everything in pen I added during the lecture.
I’m one of those nerds who likes to have just the right pens (Marvy Le Pen) and notebooks (Miquelrius A4 Quadrile), so at first I was a little disappointed that the instructor was providing some of this for me. Her reasoning, as I remember, was as follows: So much material is covered during each class period that you’d have to write furiously nearly the entire time to get everything down. But writing furiously is not the same thing as learning. Learning, like digestion, takes time. Having the notes partially completed (scaffolded) allowed some time to breathe and process.
There were other benefits, too. One was that the critical formulae and terms were already written out, so there was no risk of copying (and memorizing) them incorrectly. If I wanted to get a head start on a section, I could look through the notes and get a pretty good idea where she was going to go in class. And if I missed a class, I could find the notes (the scaffolding plus what she’d completed in class) online. It’s a good system, and one that I plan on employing once I’m teaching again.
Managing Math Phobia
One of Mrs. Grady’s common refrains was: “This is something I’ll expect you to be able to do on a test.” Or, conversely: “This isn’t something I’ll expect you to be able to do on a test.” The tactic seems to be to cover harder versions of a problem in class and in homework and then lighten up a bit for the quizzes and exams, when students aren’t able to get help. This is fine, but it can make the material seem insurmountable. Being clear with students about expectations and what they should be able to do alone versus what they may need help on goes a long way in making math seem more approachable.
Another thing Mrs. Grady did that made the classes seem more approachable was to weight the grading such that you could still pass the class even if you bombed one test. No one should fail a class just because of one bad day.
Every so often, while working a problem on the overhead projector, Mrs. Grady would look up at the class and say something along the lines of: “Do you remember when this part of the problem [factoring, say] used to be the whole problem? When you used to have an entire test just on this? Now it’s no big deal.” This whole “looking back on where you’ve come from” is critical in all parts of life, especially the parts that seem to lend themselves to frustration, or a feeling that you’ll never really “get it.” Math qualifies on both counts.
Preparation
As these were the first calculus classes I’d taken in over two years, I was worried that I would have forgotten too much to be able to continue in the series. So I made a bunch of new flashcards and reviewed old ones, practiced problems on Khan Academy, and read a great book called Calculus for Dummies.
This preparation ended up being more than sufficient. In fact, I was amazed at how much I’d retained. On the first day of class the instructor handed out a review with simple directions: “If you struggle a bit with this review material,” she said, “that’s normal. You’ll catch up and be fine. On the other hand, if you find this impossibly difficult, you might not be ready for this class.”
I found the exercises challenging, but not impossibly so. I’d held onto a bit from my previous courses and was able to dredge it back up through my review.
Assignments
There were three types of assignments: in-class activities, regular homework, and graded homework.
In-Class Activities
These were usually completed in class with other students. They provided an opportunity to work through the material while peers and the instructor were available to help.
Homework
Just a dozen or so problems from each chapter. In Calculus III, the instructor checked these every few days, but we never turned them in. In Calculus IV we did turn them in, along with a coversheet on which we wrote an observation and a question about the material. I liked the practice of deliberately writing down an observation and a question, but I wondered if this added unnecessary overhead for the instructor, compared with just glancing over the completed homework in class. That said, I definitely took the homework more seriously when I knew I’d have to turn it in.
Graded Homework
This was similar to the regular homework, except that we were to focus on presentation and clarity. Assignments were due about every week and a half, and consisted of three assigned problems to be completed in detail, such that anyone with a basic understanding of the subject matter could read through the solution and understand how the problem was solved. Mrs. Grady encouraged us to use LaTeX on the graded homework if we were so inclined. I’d used it once before during CS 225 at Oregon State, but found it so tedious and laborious that I’d gone back to pen and paper. This time, however, I was committed to learning LaTeX and using it for each of my assignments.
I settled on a template I’d found online and used a service called ShareLatex for editing. Using LaTeX was slow-going at first, but once I figured out the most common commands (how to use math mode, special characters, etc.) I found that it didn’t take me much longer to use LaTeX than to use pen and paper. And even if it did slow me down a bit, it was a positive change. As I’ve written in other class review posts, learning takes time. Not time spent banging my head against the wall, but time to process and digest. Using a slightly slower method like LaTeX makes room for that passage of time so that I can really learn and understand the material. All of that said, my favorite part about using LaTeX is that the final product is just so damn pretty:

Exams
There were four exams for each course. Two standard, midterm-style exams, one take home exam, and a final. For Calculus III we were given a formula sheet for each exam, but for Calculus IV we were expected to make this formula sheet ourselves and use it during the test, like a cheat sheet. I like making cheat sheets, but I always had a sneaking suspicion that I’d left off an important formula. Because of that, I think I prefer having an instructor prepared formula sheet over making my own. But I probably learned more by having to make on myself.
Mrs. Grady prepared a set of review problems for each exam, which I found very helpful. In fact, the only studying I did was to work through the review problems. Once I knew I could complete those problems without issue, I was confident that I could do well on the exam. And if ever I had to look up a formula, I knew that it needed to be on my cheat sheet (or memorized if it weren’t on the provided formula sheet).
Extra Resources
I found the classroom instruction and textbook (Stewart) sufficient for nearly all the material. YouTube and Mathematics on StackExchange filled in the gaps. I also found Desmos helpful for Calculus III and GeoGebra.org/3d helpful for Calculus IV.
Difficulty and Time Commitment
I spent 125 hours on Calculus III and 100 hours on Calculus IV, which both included about five hours per week of classroom instruction, and in the case of Calculus III, approximately 25 hours of preparation time before the course began. On average, this works out to about 12 and 10 hours per week over the course of the terms, respectively.
For what it’s worth, each term I took two other courses at Oregon State. I also take care of my one-year-old daughter (along with my wife and in-laws) and volunteer one afternoon each week at a local high school teaching computer science.
Final Grades
- Calculus III: A
- Calculus IV: A