One of three courses I took this term was on Ring Theory, the sequel to Group Theory, which I took last term. Besides the subject matter, there were a few minor differences between the two courses which I’ll highlight below. Most everything else, like the text and the instructor, remained the same.
Instructor
Dr. Julie Bracken
Subject Matter
As I wrote above, this course came right on the heels of Group Theory, which deals with the same idea. The main difference is that instead of dealing with groups (which are basically an operation, like addition, paired with a set of elements), we focused on rings (which are again a set of elements, but now paired with two operations, say addition and multiplication).
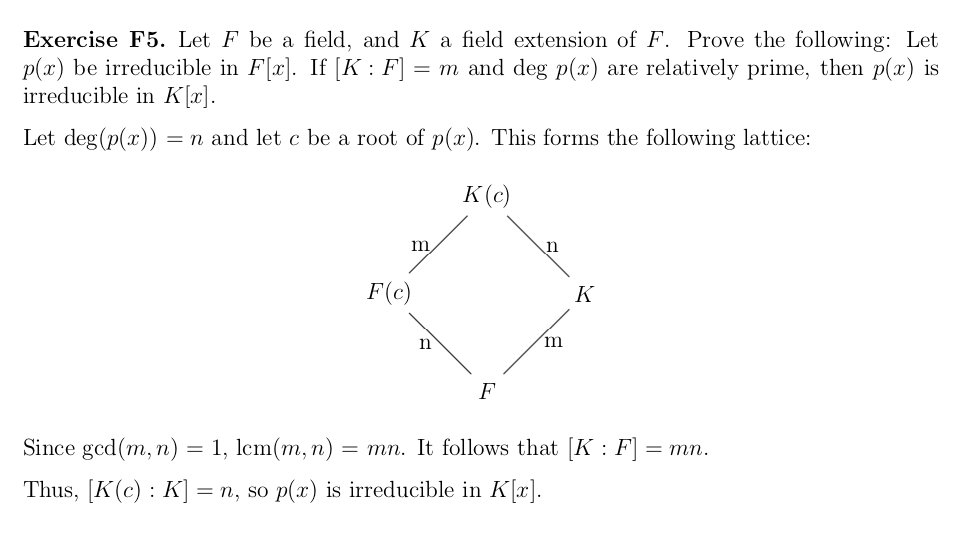
As you might expect, there’s a ton of overlap between the two subjects, but it is in ring theory that the “excitement begins” (according to the author). Ring theory allows us to see why the Greeks were unable to trisect an angle or double a cube. It’s also the introduction to Galois Theory, which unfortunately we only had a few days to cover.
Preparation
I went straight from group theory into ring theory, and thank goodness. Had I taken more than a term or two off between the courses I think I’d have been sunk.
Text
This course continued with Pinter’s A Book of Abstract Algebra. We started with Chapter 17 and continued through Chapter 32.
When I used the text last term I didn’t want to highlight in it for fear that I’d damage the resale value. This term I got over it. Also note my homemade paperweight, which represented a great leap forward for Alex-kind.
I still enjoyed the book, but I often wished that there were more examples and more detail. For what it’s worth, Dr.Bracken said that John B. Fraleigh’s A First Course in Abstract Algebra is another good introductory text.
Lectures
The lectures were structured exactly as they were in Group Theory. The only difference is our class periods were two hours long (twice the length of Group Theory) and only two days a week (instead of three).
Last term I used a wirebound notebook from MUJI. This term I switched to looseleaf printer paper which I turned into dot paper with help from Incompetech.
Dr. Bracken always set aside about five minutes in the middle of the period for people to go to the bathroom, get a drink of water, etc. I think taking breaks during long class periods is one of the best and easiest things instructors can do to enhance the learning experience. I don’t know if it actually increases retention, but I do know that I enjoyed the class much more when I could step away for a moment before jumping back in.
Strategy
The only modification I made to my strategy this time around was to make more flashcards, and to make them more regularly. Here’s the deck I created over the course of the term.
In Group Theory I’d make a set of flashcards before each exam and then try to cram them into my brain before test day. This time around I made flashcards on an ongoing basis. I’d do this by highlighting the passages as I read a chapter and then going back through and turning those passages into flashcards. This usually resulted in about fifteen to twenty flashcards for each chapter.
I’d then review these flashcards on as close to a daily basis as I could manage. I did the same thing for my other two courses this term (geometry and statistics), and so usually ended up with about twenty minutes worth of flashcards to review each day.
Assignments
Not much changed from last term. We had six assignments instead of five, and each of them usually took me a day or two to finish. I completed them using LaTeX and Overleaf.
I’ll be damned if LaTeX doesn’t make for the prettiest homework assignments you’ve ever seen.
Exams
Just like last term, we had two exams and then a final. I earned an A and a B on the exams and then a B on the final. Each consisted of four or five things we had to prove or show.
For the first exam, we were given five problems and then told to answer any four. I really appreciated this since each problem carries a tremendous amount of weight in the final grade for the course. On the final, for example, each problem is worth 8 percent of the final grade!
Unfortunately, choosing to drop one question was only an option for the first exam. And I can imagine why: it’s probably considerably more work to grade, and it doesn’t get around the fact that it’s a difficult course with difficult material. No amount of testing or grading modifications can change that.
Beyond being able to drop a question, I found the tests quite difficult. On the final, for example, I remember thinking: “I have no idea how to solve any of these problems.” But I focused on what I knew and worked the problems step by step and then eventually came up with what were (apparently) satisfactory responses.
Onward
One day while I was doing homework for this class I came across the following quote (which I’ll attribute to Kaj Hansen):
“Math is torture. Our mathematical proficiency is proportional to the extent we have tortured ourselves.”
This class, coupled with my other courses and obligations, sometimes amounted to torture. Not because of the instructor, or the text, or (I hope) my own intellectual inadequacy, but because it’s hard. And as the quotation alludes to, there’s not much that can be done about that.