One of three courses I took this term was called Modern Geometry, which covered Euclidean geometry, taxicab geometry, hyperbolic geometry, and spherical geometry.
The majority of the course focused on the first subject, though, so I think better titles might have been “Axiomatic Geometry” or “Euclidean Geometry.”
Instructor
Dr. Steve Boyce
Subject Matter
This course covered a variety of topics related to Euclidean and other geometries:
- Axiomatic systems
- Transformations and congruence
- Synthetic geometry
- Area
- Similarity
- Circles
- Finite and analytical geometry
- Isometry and symmetry
- Taxicab geometry
- Hyperbolic geometry
- Spherical geometry
One thing that was explicitly excluded from the course was trigonometry, which deals with the relationship between the side lengths of triangles and their angles.
Preparation
I read a big chunk of Euclid’s Elements when I took History of Math last term, but beyond that I hadn’t had any exposure to geometry since high school.
Lectures
This class was dynamic and interactive, which made it the polar opposite of the other courses I took this term on abstract algebra and statistics, which were solely made up of a series of lectures. By and large I liked the constructivist approach applied by the instructor, but there were times during the course when I wished that he was a little bit more direct in his teaching of the material.
To give a concrete example, early on in the class we were asked to determine whether an angle of zero degrees was still an angle. As a class, and without the instructor’s direction, we decided that a zero degree angle was in fact an angle.
Whether this trivial case was actually included didn’t make much of a difference in how the class unfolded, which explains why the instructor left the decision up to us.
Most of the notes for this class were provided. I only ended up taking a few pages of notes on my own.
Now, in retrospect, I can see the value in leaving this sort of decision up to students since it puts them in the shoes of someone (like Euclid) who’s deciding the boundaries and definitions of an axiomatic system.
Strategy
In a word, flashcards. I made an Anki deck for the class and added every term and idea from the notes to it. This amounted to 314 cards, many of which contained images that I made with GeoGebra. If you’re interested in the deck, you can download it here.
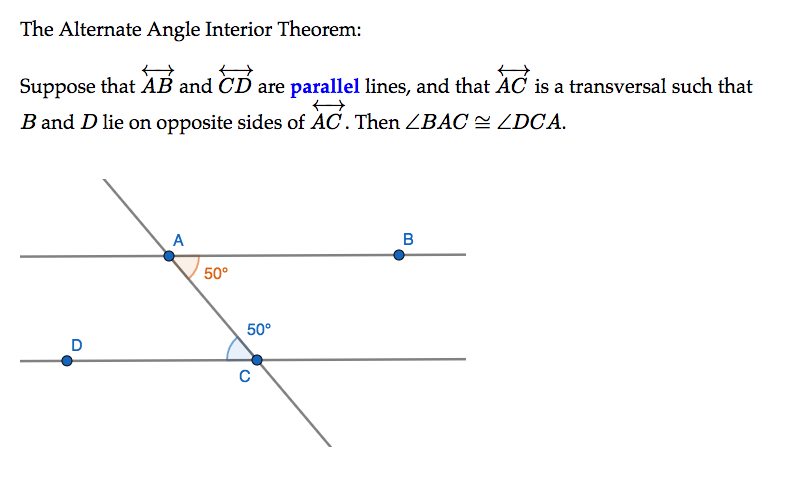One of the flashcards I made for the course. In this case, the text in blue would’ve been hidden until I guessed the answer and clicked to reveal it.
I set a reminder on my phone to do flashcards every day. I set the limits on the app so that I would have about 10 or 20 minutes worth of flashcards to do each day. I did this in my other two classes, too, so I usually ended up with half an hour or an hour worth of flashcards each day. This was my primary means of studying material.
Assignments
As I mentioned above, I sometimes wished that the instructor was more direct. This was particularly true when it came to questions I had on the homework, which were often met with well-intentioned but ultimately unhelpful responses. Finding the balance between guiding too much and not enough is tremendously difficult, though, so I would expect any instructor to struggle with this from time to time.
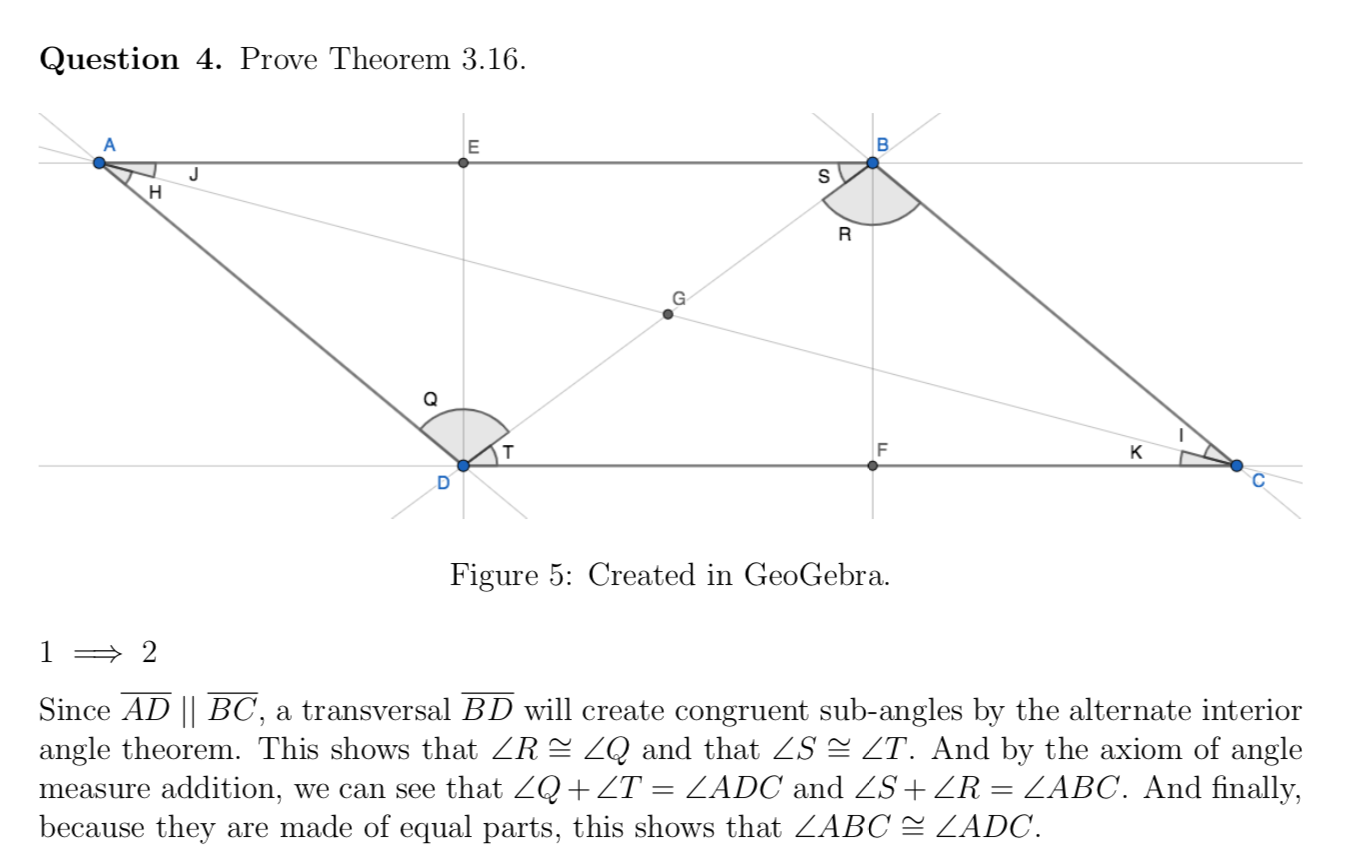It’s possible to create diagrams and images in LaTeX, but in the interest of time I made most of my drawings in GeoGebra and then imported them as images.
Exams
There were three exams in the course, two midterms and one final. I don’t remember much about them (I’m writing this a month after the end of the class), except that I used all of the time available, as I almost always do.
Onward
As I wrote at the top of this post, it had been over a decade since I’d done much of anything with Euclidean geometry. This class was a fun introduction, and I enjoyed getting back into geometry without simultaneously tackling trigonometry (sine, cosine, tangent, etc.).