Last week I covered the math of Ancient Greece. Fast-forward about 1,500 years and we’re in the Italian Renaissance, the period which ushered in dramatic changes in art, science, politics, the economy, and of course, mathematics. The three most significant changes, covered below, were the pursuit of formulae for higher order equations (i.e., moving beyond the quadratic formula), modernizing and standardizing mathematical symbols, and coming to a consensus on what seems like a trivial question: What is a number?
Unless otherwise noted, my summary and commentary below is based on A History of Mathematics by Victor Katz.
From Quadratics to quartics
One way to categorize equations with unknowns is to group them by the degree of the unknown. The lowest degree, like x = 12, are known as linear equations. Raise x to the second power and we have a quadratic equation, like x² = 9. Raise it to the third power and we have a cubic equation, like x³ = 8. Raise it once more, to the fourth power, and we have a quartic equation, like x⁴ = 81. Finding the values of the unknowns in equations like these has been a focus of mathematics since the time of the Babylonians.
The Babylonians, active a couple centuries before the common era, were able to apply a formula to solve linear and quadratic equations. The modern quadratic formula, employed to solve an equation of the form ax² + bx + c = 0, looks like this:
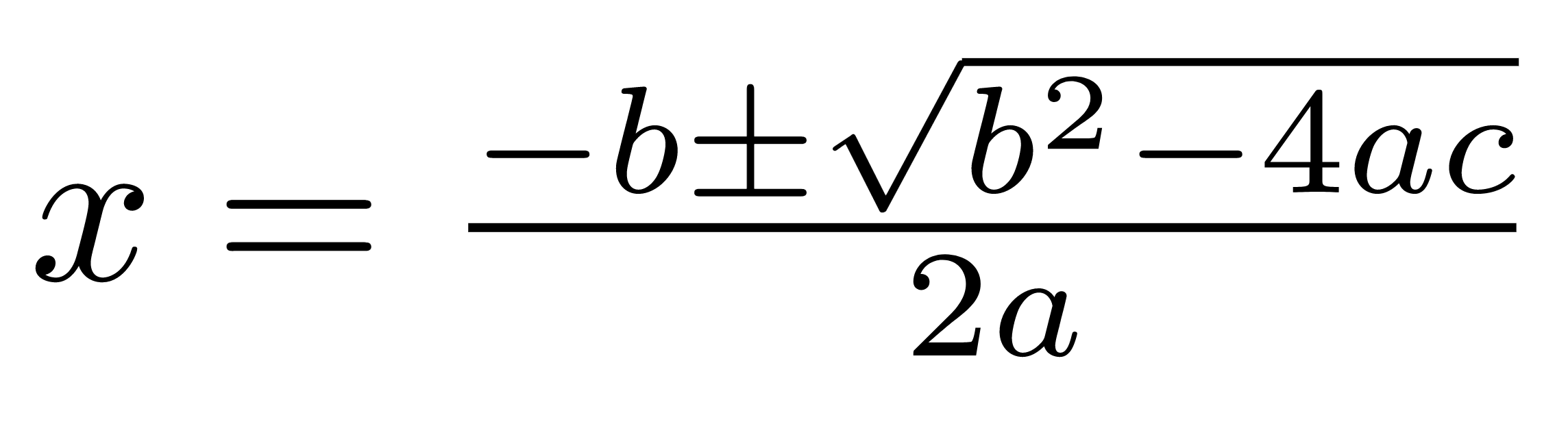The quadratic formula. Substitute a, b, and c, and voilà, you have your x.
Other cultures around the world achieved similar feats, probably in independence. But it would be several thousand years before anyone worked out a formula for solving equations of the third and fourth degree, the cubics and quartics mentioned above.
Abacists and the economy
When we consider the Renaissance, we’re quick to think of developments in art and science, and of the characters who embodied both, like Leonardo da Vinci. But there were other changes afoot.
Europe was moving out of its medieval, barter economy, and into a more modern economy based on money. The businesses themselves were becoming more sophisticated, too. Instead of one-off ventures in which someone would commandeer a ship and crew to bring foreign products to market, businesses were forming which made possible a continuous flow of goods between ports.
Double-entry accounting, an error-detection tool which is still used to this day, was first codified during the Renaissance (though it may have been invented earlier).
These changes in business came along with a new class of tradesmen: abacists. Part accountant, part mathematician, part instructor, the abacists bear much of the responsibility for the mathematical developments of the Renaissance. Why? Because they pushed forward the study of mathematics and passed it on to their students.
Higher order equations
The abacists used Islamic and Greek math as their foundation and then built from there. In terms of finding general solutions to the cubic and quartic equations discussed above, there were a number of players involved. The most famous of these was Girolamo Cardano. In addition to being the foremost mathematician of his era, Wikipedia credits him with being a physician, philosopher, gambler, and, inexplicably, “supporter of the witch hunt.”
In terms of Cardano’s mathematical achievements, he made use of negative numbers, acknowledged the existence of imaginary numbers, and published formulas for cubic and quartic equations in his seminal book Ars Magna. The key word there is published, since the formulas were not originally created by Cardano. One came from his predecessor Scipione del Ferro, and another from his assistant, Lodovico Ferrari. Cardano attributed the work of both in his book.
Perhaps the most famous of Cardano’s appropriations were the formulas of Niccolò Tartaglia. Tartaglia shared his cubic formulae (in the form of a poem!) with Cardano on the condition that Cardano not publish them. It turned out that del Ferro (mentioned above) came to the same solutions as Tartaglia, which Cardano felt entitled to publish. Still, Tartaglia felt he’d been betrayed, and the episode kicked off a feud that would last the rest of their lives.
Modernizing marks
Perhaps the most striking realization I’ve had in spending the past few weeks studying the history of math was that its representation was not born fully-formed. The first numbers bore no resemblance to our own, and the same holds for our symbols. In other words, the first addition that was ever written wasn’t “2 + 2 = 4.” Instead, it was probably more akin to “take two of a thing, add to them another two, and the result is four.”
Some of the most important developments of mathematical symbolism came out of the Renaissance (just check out the number of symbols on this page which originated in the 15th and 16th centuries). I’ve highlighted a few below, which, along with others, culminated in what we now understand to be modern algebraic symbolism in the mid-seventeenth century.
From Roman to Hindu-Arabic numerals
What’s XXIX times XVII? Why, CDXCIII, of course. In case your Roman numeral multiplication is a little rusty, that’s 29 times 17, which equals 493. Worse yet, what would that result multiplied by ten be? In our modern Hindu-Arabic numerals we just add a zero at the rightmost position: 4930. But in Roman Numerals it changes the number entirely, from CDXCIII to MMMMCMXXX.
Needless to say, a place-based system (whether decimal or not) which employed zero as a place value offers huge advantages over a non-place-based system. Still, Arabic-Hindu numerals were not adopted immediately. Why? Katz writes: “It was believed that the Hindu-Arabic numerals could be altered too easily, and thus it was risky to depend on them alone in recording large commercial transactions.” If this seems quaint, think about the last time you wrote a check. You likely wrote out the value twice, once using numerals ($17.50) and again using English words (seventeen dollars and fifty cents).
Algebraic symbolism
Just as the the Renaissance was brining changes to the representation of numbers, mathematical symbols, like + and -, were changing too. But this was a slow, iterative process. An intermediate step, near the end of the fifteenth century, involved replacing the Italian words for plus and minus with the abbreviations of p̅ and m̅.
It’s worth noting that calling symbolic notation or a place-value number system an “advancement” is at least partly subjective. Just as we find the Roman numeral system to be foreign and difficult, mathematicians of that era would likely have judged our numbers and systems similarly. It just depends on what one is familiar with.
Other mathematical symbols were standardized during this era. Among them, the (totally radical) symbol √ for square root, which is credited to the German mathematician Christoff Rudolff, the symbol = for equality, credited to the Welshman Robert Recorde, who wrote of the two parallel lines that “no two things could be more equal.” Rafael Bombelli, the Italian mathematician, wrote powers as a superscript relative to the entity being raised (though next to the number, rather than the variable). And the Frenchman François Viète used letters to represent unknowns in algebraic equations, an innovation whose utility and importance speaks for itself.
Finally, Simon Stevin developed and advocated for a notation for decimal fractions which bear a striking resemblance to our modern notation. In Stevin’s notation, which he called “decimal numbers,” the number 123.875 would be written 123⓪8①7②5, rather than as an integer summed with traditional fractions, 123 ⅞. According to Katz, “He also played a fundamental role in changing the basic concepts ‘number’ and in erasing the Aristotelian distinction between number and magnitude.” I’ll get to these concepts in the next section.
Unifying number and magnitude
The Greeks had some interesting ideas about different types of number. They drew stark a distinction between discrete numbers, which they placed in the category of “number,” and continuous numbers, like √2, which they called “magnitude.” The two types behaved differently in different situations, hence the distinction.
Stranger still, the Greeks even drew a distinction between 1 and numbers greater than 1, arguing that 1 (unity) is simply a generator of numbers, as the point is the generator of a line. Stevin, mentioned in the previous section, was sure that 1 was a number like any other. So sure, in fact, that he wrote “THAT UNITY IS A NUMBER” in his l’Arithmétique. Stevin also worked to remove the distinction between number and magnitude, though it would be several more centuries before discrete arithmetic and continuous magnitude found their union. Still, Katz writes, Stevin’s contribution was significant: “Ultimately, [Stevin] was so successful that it is difficult to understand how things were done before him.”