In my previous posts on The Crest of the Peacock by George Gheverghese Joseph, I summarized the mathematical developments of several pre-Colombian American cultures and of the Egyptian and Mesopotamian cultures.
In the case of the former, it was clear that the math that developed there did so in isolation. In the case of the latter, we can trace clear connections with the West. China, where the book next turns its focus, is more ambiguous.
We know there was considerable transmission of goods between East and West. In addition to making possible the trade of goods, the Silk Road also made possible the spread of culture, and even disease. Unfortunately, the transmission of ideas is much harder to trace than the transmission of goods, so we’re left wondering who influenced whom, and how.
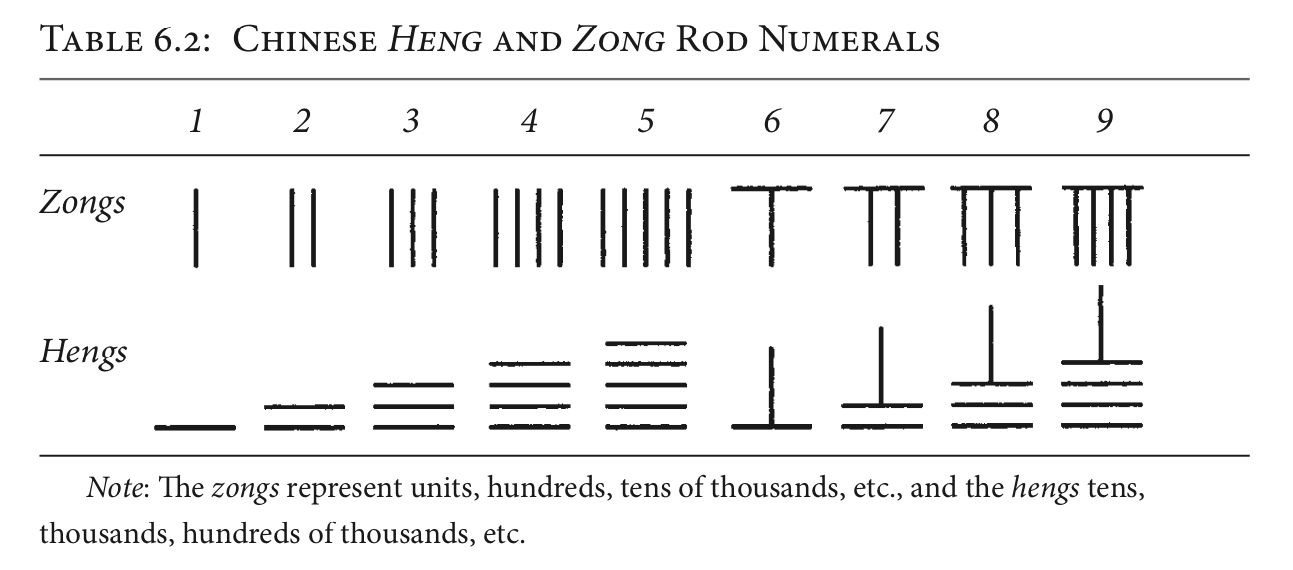
Rod numerals
There were several numeral systems active in China, but the one I’ll focus on here is rod numerals, which date to around the second century B.C., or perhaps earlier. The numeral system itself appears to have grown out of the practice of using counting rods for calculation. These were small pieces of ivory and bamboo, and were arranged in columns from right to left, each representing increasing powers of ten. This made the counting rods a place-value decimal system of numeration.
Taken from The Crest of the Peacock by George Gheverghese Joseph.
Rather than using the same set of symbols for each place, however, the Chinese alternated a different (though similar) set of symbols for neighboring places. In other words, units, hundreds, ten thousands (and so on) used one set (zongs) while tens, thousands, hundred thousands (and so on) used another (hengs). This focus on opposing or alternating entities may have been rooted in the Chinese philosophy of yin and yang, but this is just conjecture.
Negative numbers were denoted with red counting rods, and fractional parts were divided from integral parts with a vertical line.
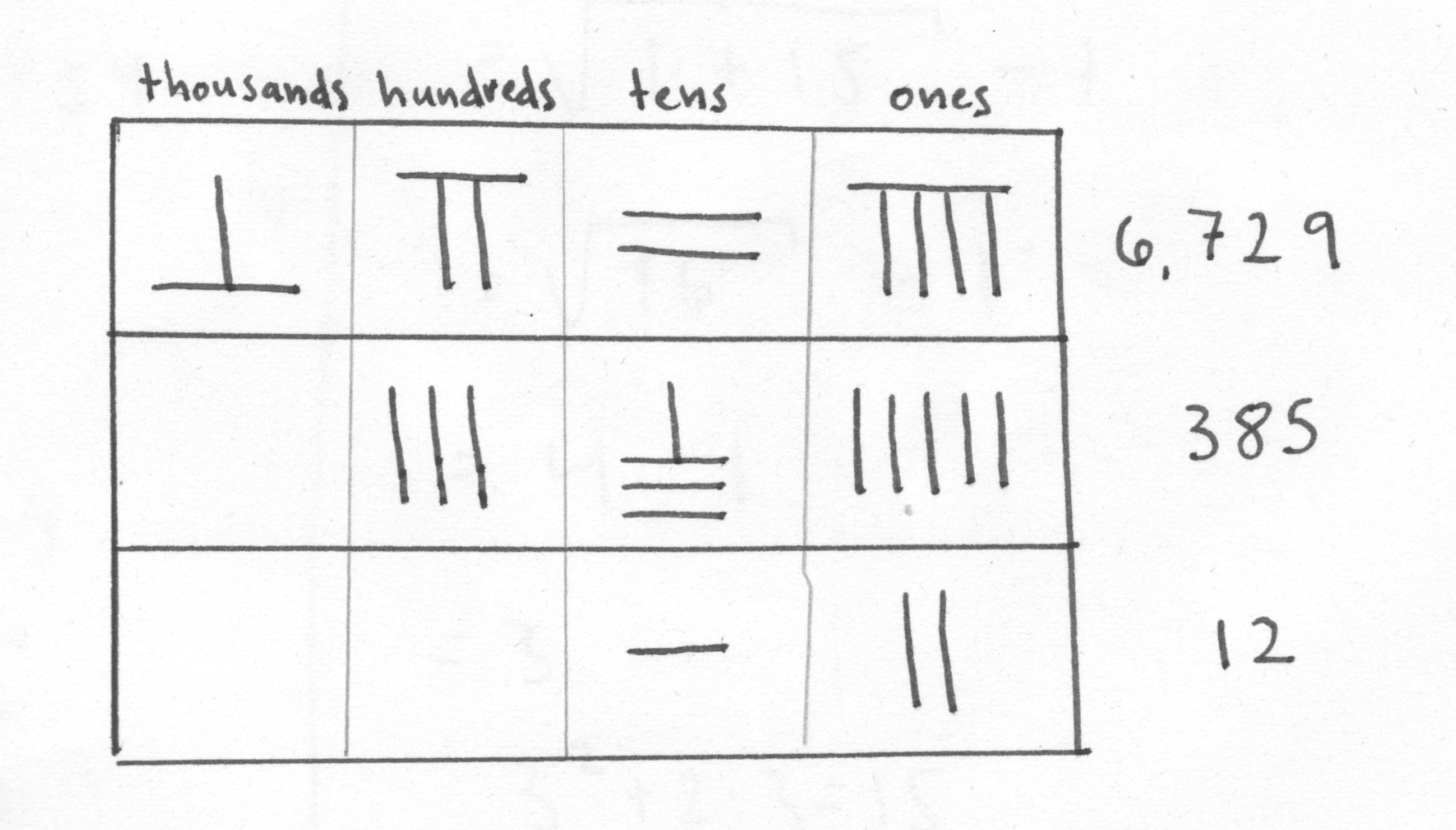A few numbers written in heng zong numerals. Note that the rods in each column are oriented similarly. This probably wasn’t a mistake, as it would help ensure that numbers were arranged in the proper place.
While it is less ambiguous than the Egyptian and Mesopotamian systems, some problems remained. For example, how would one differentiate between the numbers 12 and 1002 without a symbol for zero? In this situation, a space was used to represent the “empty” columns.
It’s important to point out that the counting rods were used primarily to calculate numbers, unlike the quipu of the Inca, which were used to record numbers.
There’s no conclusive proof that this place-value decimal system influenced other traditions outside of China, but the author does point out that the methods employed by the Persian Al-Khwarizmi were “almost identical to the Chinese procedure.” The central issue with this theory rests in explaining how a system that depended on the manipulation of physical objects (counting rods) was adapted into a system that existed only in writing.
Lao Zi, the Chinese philosopher active in the 5th century B.C., is credited with the phrase “good mathematicians don’t use counting rods,” but based on the following, you might come to disagree.
Magic squares, magic circles, and other magic
A magic square is an arrangement of numbers 1 through n in a square such that each row, column, and diagonal add up to the same number. Here’s an example:
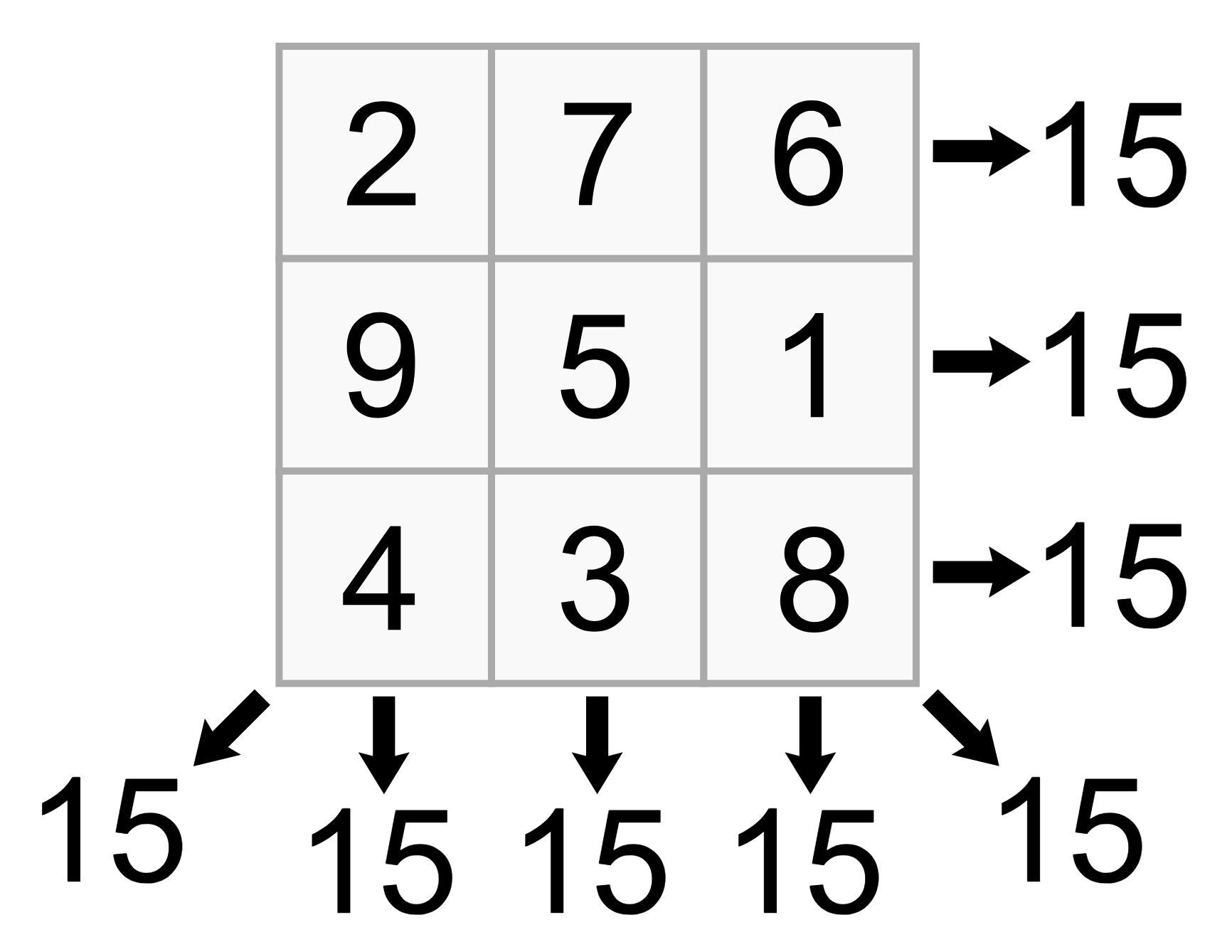The squares are filled with the numbers 1 to 9 and each row, column, and diagonal add to 15.
They originated in China around the second century B.C. before spreading to India, the Middle East, and other parts of the world. They can be created according to formulae, and Yang Hui, writing in the 13th century, expanded the process of creating magic squares to the orders of 3, 4, and 5 (meaning a square with 5 numbers on each edge). He then went on to describe the creation of magic squares of orders up to 10, though the book notes that these descriptions were incomplete. Nowadays we know that there exists no upper limit on the size of magic squares. The current record (according to one website) for a printed square is 3,559 x 3,559 and contains 12,666,481 numbers.
Yang Hui also described several magic circles, which are an arrangement of numbers such that each number lying on a series of concentric and overlapping circles, plus the circle’s diameter, adds to the same number.
The ability of Chinese mathematicians to create these magic squares speaks to a strong grasp on computation, no doubt aided by their employment of counting rods. However, this facility with counting rods may have held back other advancements. I’ll get to that shortly.
Jiu Zhang
Also known as The Nine Chapters on the Mathematical Art, the Jiu Zhang is described by Joseph as “one of the oldest and certainly the most important of the ancient Chinese mathematical texts” and probably comes from around the first century A.D. It’s laid out as a series of problems and covers a variety of topics, including:
- Addition, subtraction, multiplication
- Manipulation of fractions
- Geometry, in which π is estimated to be 3
- Calculating the volumes of different solids
- A formula for finding square and cube roots
- Solving two equations with two unknowns
- Matrix manipulation
- Solving systems of linear equations
- Pursuit problems
Pursuit problems involve those in which one is asked to calculate something like when a train leaving San Francisco at 70 miles per hour will cross paths with a train leaving Chicago at 65 miles per hour. Perhaps some solace can be taken in the fact that this sort of problem has been troubling students the world over for the better part of 2,000 years.
In the case of matrix manipulation, the author writes that this development may have been a natural outgrowth of the use of counting rods, since the same methods don’t show up in other cultures until the advent of modern math. Conversely, the reliance on these same techniques may have also inhibited other developments, like that of abstract algebra.
A similar point the author makes in this section is that while the Jiu Zhang was revolutionary for its time, it may have also held future Chinese mathematicians back. Joseph writes:
Its influence on the Song mathematicians of the thirteenth century was perhaps even counterproductive, since they were obliged to refer to it, just as some of today’s academics routinely cite standard authorities to make their work “respectable.”
Pythagoras in China
The Pythagorean Theorem, which describes the relationship between the sides and hypotenuse of a right triangle, is credited to the ancient Greek of the same name. But many cultures discovered this relationship independently, including in China, where it is known as the Gougu Theorem. A visual proof for the theorem dates to around 300 A.D.
Slicing pi
Liu Hui, writing in the third century A.D., achieved an estimate of π accurate to the thousandths place (3.1416) using polygons of known perimeter inscribed inside of circles. A couple hundred years later, Zu Chongzhi and his son Zu Ghengzhi calculated π to the seventh decimal place, a level of accuracy that stood for hundreds of years. Unfortunately, their methods of calculation are unknown.
What makes a good mathematician?
As I wrote above, Lao Zi said “good mathematicians don’t use counting rods.” My first response to this statement was absolute disagreement (hence the title of this post). There can be little debate that counting rods facilitated computation and helped push Chinese mathematics forward.
But what if Lao Zi was actually saying that good mathematicians look beyond counting rods (and computation). What if the definition of a good mathematician was simply one who was capable of abstraction?
There are hints of this world beyond computation in calculus, and even more in linear algebra. Indeed, I’ve grown to love math as an adult largely because I’m focusing more on abstraction and less on computation. And I think a big part of that is that abstraction, not computation, is the core of mathematics.