For many people, the basic story of the history of mathematics is that Greeks came up with a bunch of cool stuff, it was forgotten for a long time, and then Europeans rediscovered Greek knowledge and ran with it from the Renaissance onward. But maybe that’s not exactly right.
The problem with this belief is two-fold. One, the Greeks themselves described the debt they owed to their predecessors (the Egyptians) for their mathematic progress. And two, we now know that there were high-level mathematics being practiced in Egypt and Mesopotamia before the Renaissance.
Beyond that, this also supposes a linear development of a singular mathematical entity. In reality, mathematics is made up of many different parts. There are number systems, operations, practical applications, and so on. And while it may be simpler to think of mathematics as a single torch that was passed from one culture to the next (Egyptians, perhaps, then to the Greeks, and finally to Europeans and the west), different mathematical fires have been lit and extinguished for thousands of years, some joining together and others left to burn on their own.
So begins The Crest of the Peacock, a book by George Gheverghese Joseph which serves as the primary material for an independent study I’m completing this term on the history of mathematics. Each week I’ll be writing posts about what I’m learning and sharing them here.
The second chapter of the book, entitled “Bones, Strings, and Stones,” traces mathematical development that appears to have existed in isolation of the developments in Egypt, Mesopotamia, and Greece. In particular, the author explores the Ishango bone found in what is now the Democratic Republic of the Congo, the quipu knot system employed by the Inca, and the number systems of the Maya and Aztec. I’ve included some thoughts on each.
The Ishango Bone
This tool made from a baboon bone, pictured below, is believed to be at least 20,000 years old. A piece of quartz is fixed to one end, and all along the side are what appear to be deliberate notches cut into the bone itself. Perhaps they represent tallies, or some other form of counting system. Or maybe the bone shows the practice of a proto-number theory, since one group of tallies contains only prime numbers. Two of tally columns add up to 60, which is about twice the length of a lunar cycle. Early astronomy? Or perhaps used to track menstrual cycles? Or maybe they don’t represent numbers at all, and were simply added to improve grip.
The Ishango Bone
The key here is that nobody knows the significance of the marks, or whether there’s any significance at all. It reminds me of trying to solve puzzles in an escape game. One of the first things you have to decide is whether something is a puzzle at all, or just some random object meant to throw you off track.
Then again, it seems implausible that behaviorally modern humans (the makers of the tool) had no need to count or to record what they’d counted. And while tally marks must’ve been invented at some point, it’s not hard to imagine the incremental development of counting on one’s fingers and then transferring that count to something more permanent. This brings me to one of my favorite lines from the chapter:
Consideration of African mathematics reminds us of what is often forgotten: mathematics is a pan-cultural phenomenon that manifests itself in a number of different ways, in counting and numeration systems, in games and leisure pursuits, in art and design, in record keeping and metrology. Our very definition of mathematics has to be broadened to include activities such as counting, locating, measuring, designing, playing, explaining, classifying, sorting.
Quipu
Quipu are strings with knots tied in them to record numbers. The Inca, who lived in and around Peru from the 13th century until the Spanish conquest in the 16th century, used Quipu to record and transmit statistical information (census data, harvest amounts, troop levels, etc). They employ a base-10 place value system in which different knots at different locations signify different numbers. Here’s what they look like:
One of the few surviving quipu
It’s important to point out that quipu were a means of recording data, not a tool for working with it, like an abacus. Here’s an example of what the number 183 might look like on a quipu:
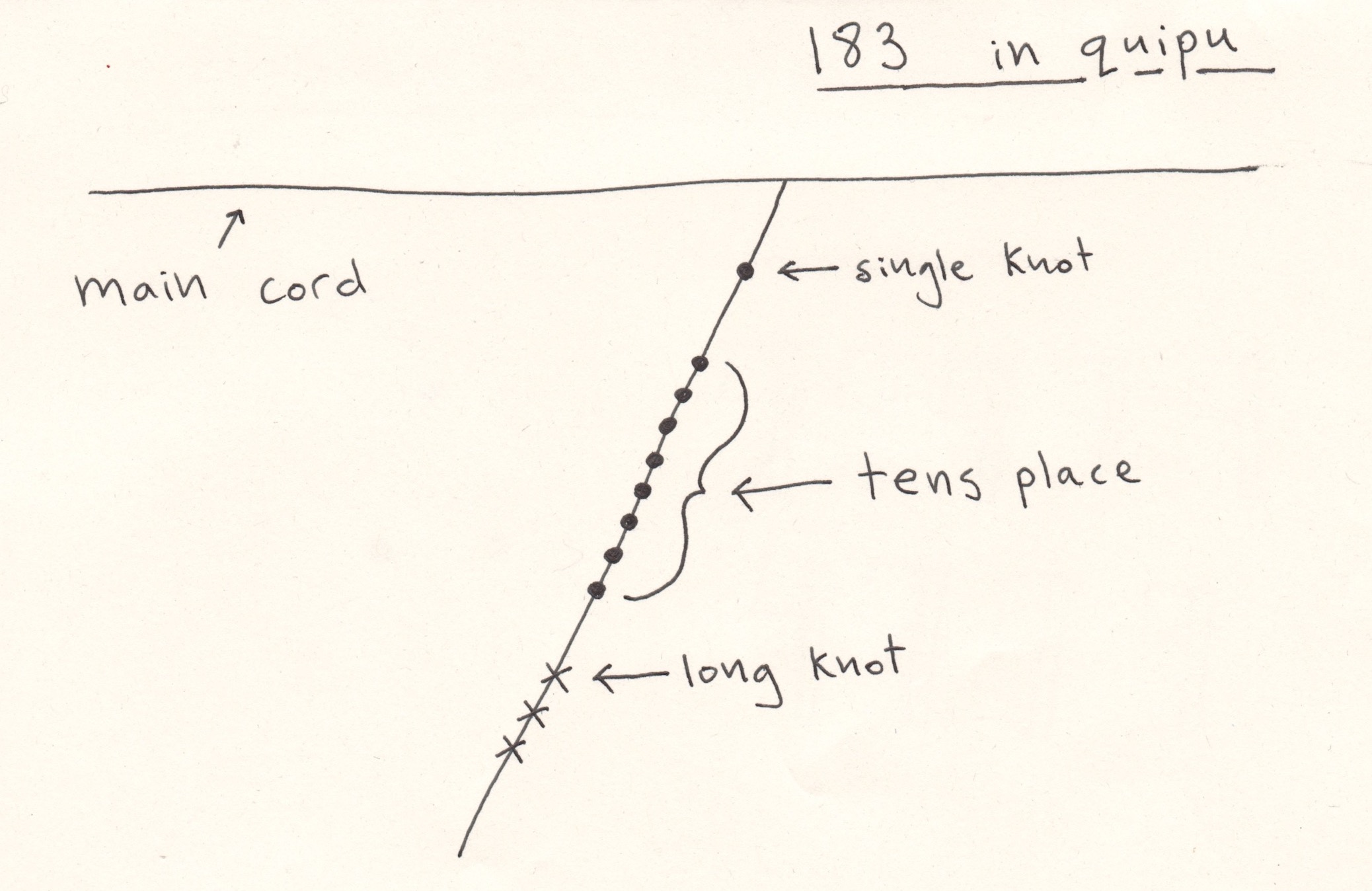The number 183 as it may have been represented on a quipu. The single knot at the top represents a one in the hundreds place, the eight knots below represent an eight in the tens place, and the three knots at the bottom represent three in the ones place.
The existence of quipu brings up an important idea that comes up several times in the early chapters of the book: in order for mathematical development to progress, a culture must have both the demand and the resources. Needless to say, coordinating an empire that stretched over 2,000 miles and included some ten million people would demand a certain level of coordination and organization, both of which would be greatly facilitated by numbers, mathematics, and record-keeping.
Mayan and Aztec Numerals
The Mayan and Aztec empires also had written number systems. The Mayan system, which predated that of the Aztec, used a base 20 place value system. They also used a shell to represent the number zero. Here’s what the numbers 83 and 38 would look like in Mayan numerals:
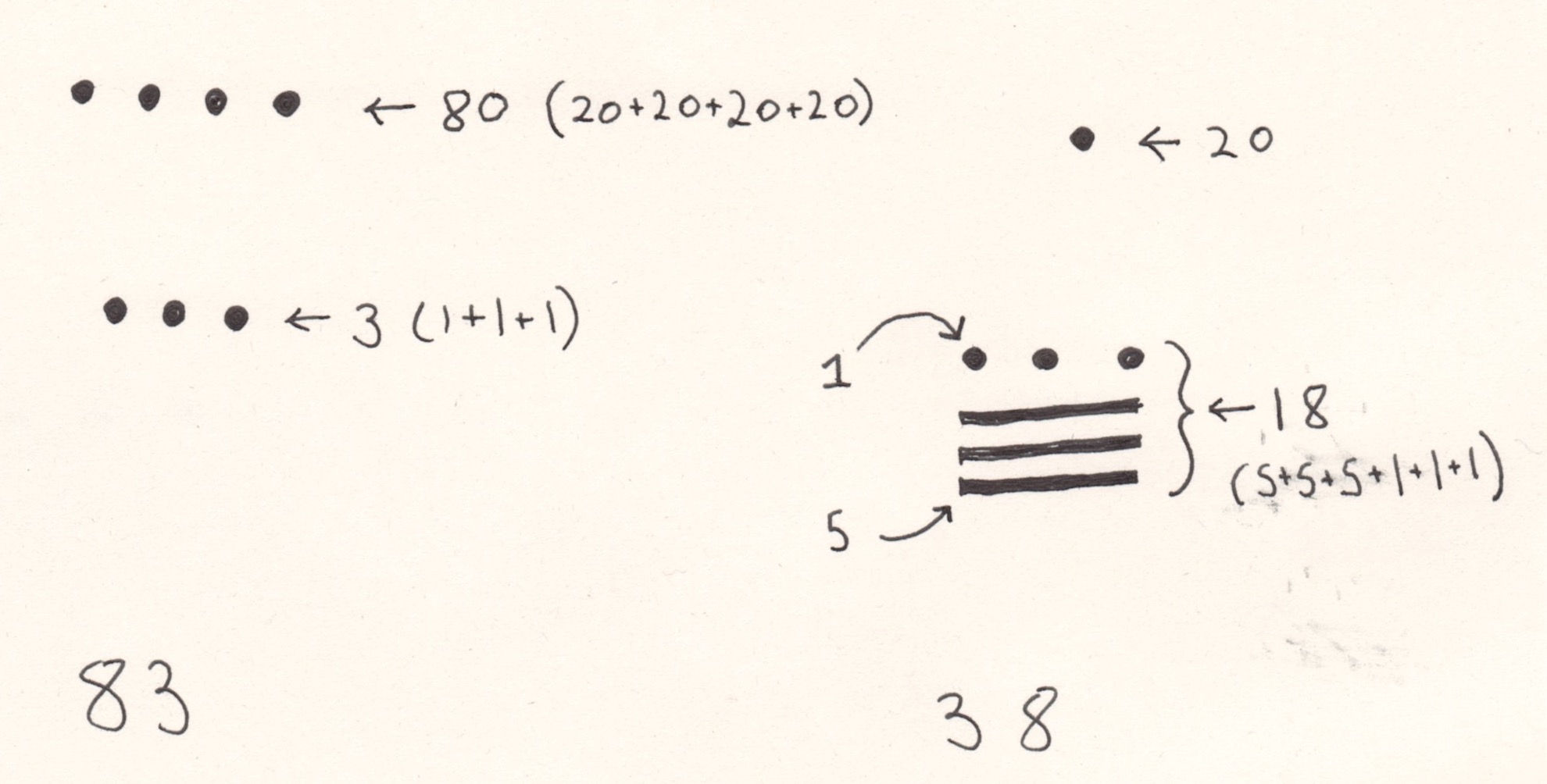The numbers 83 and 38 in Mayan numerals. The top row represents the most significant digit.
The Aztec numeral system also used a base 20 system, except with different symbols to denote different numbers, rather than different places. This is similar to the Roman numeral system. Here’s what the number 183 might have looked like in Aztec numerals:
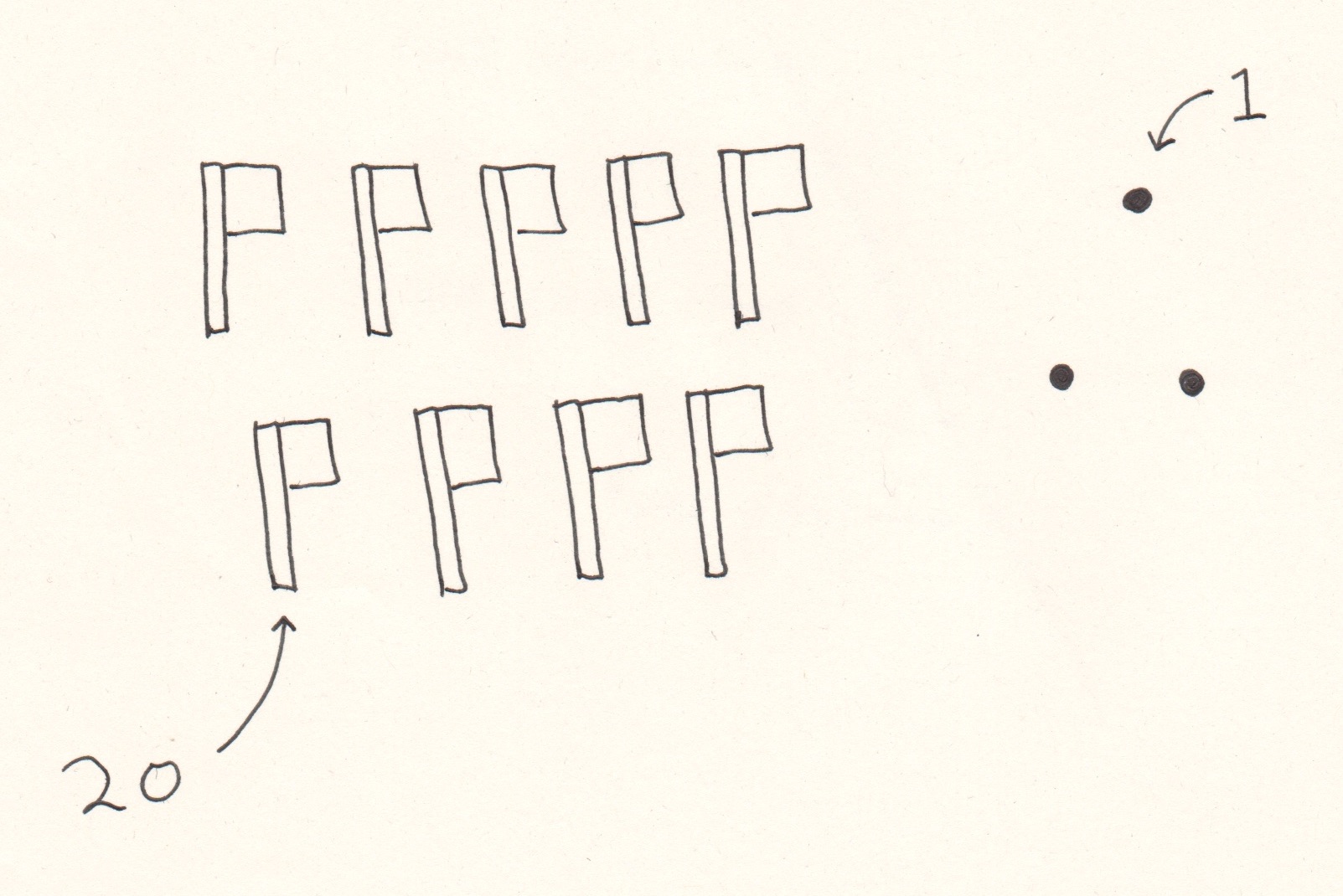The numbers 183 Aztec numerals. The flag represents the value twenty and the dot the value of one.
The Mayan and Aztec numeral systems were strongly rooted in astronomy and the calculation of astronomical events. The Mayans, for their part were able to calculate the length of a solar year and the length of the lunar month to within a thousandth of currently accepted values. They were able to predict lunar eclipses, too. Imagine the power that would rest in the hands of a ruler who could say to his subjects: “In one month, the sun will go dark in the middle of the day.” Pretty cool.
Is the concept of zero a prerequisite for a place value system?
Absolutely. Otherwise, for example, what goes in the tens place of the decimal number 101? This is not to say that a specific symbol is necessary – the Inca used a space without knots to represent zero in a particular place – but the concept of the value of zero is definitely necessary.