Calculus was invented in the late 17th century by the Englishman Isaac Newton. Or by the German Gottfried Leibniz. Or maybe their work was just a natural outgrowth of seeds sown by the Greeks two millennia before. Or maybe the Chinese and the Keralites.
Perhaps none of these statements are mutually exclusive. To see why, I’ll cover what the Greeks and Chinese knew about exhaustion and what the Keralites knew of infinite series, and then move forward to the era of Newton and Leibniz.
Measuring circles
Say you want to find the area a of a circle of radius r. You don’t have the formula a = πr². In fact, you don’t know even know a precise value for π. What do you do?
One strategy would be to draw a square inside the circle such that the four corners of the square lie on the circumference of the circle. Measure this square and you’ll have an approximation of the area of a circle. It won’t be particularly accurate (in fact, you’ll be off by more than 50 percent), but you’ll be on the right track.
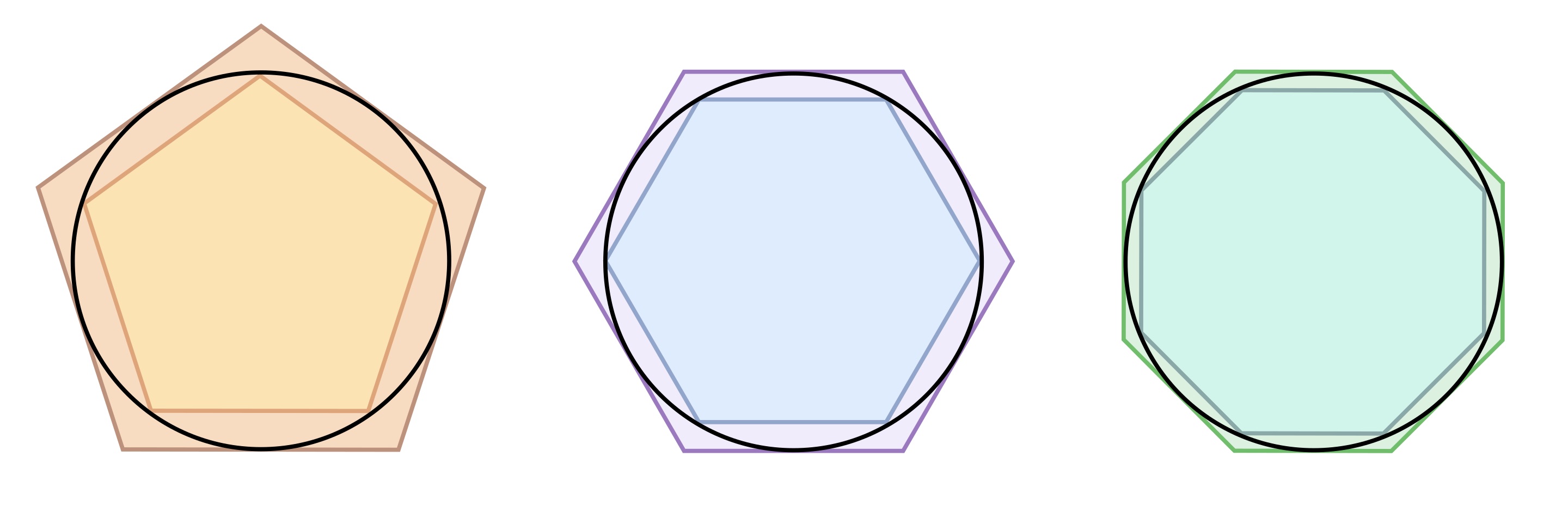An illustration of the Method of Exhaustion as applied to finding the area of a circle.
What if instead of drawing a square, you drew a pentagon? Since you can compute the areas of triangles, and a pentagon is a collection of five equal triangles, you can calculate its area. And since the pentagon comes closer to approximating the area of the circle (there’s less of area outside the pentagon and inside the circle than in our previous drawing with the square), you’re moving closer to finding the area of the circle.
The Method of Exhaustion
Taking this idea to its logical conclusion is known as the Method of Exhaustion. Archimedes used it to find the area of a circle, to find a very accurate value of π, and for other purposes besides. Several hundred years later, the Chinese mathematician Liu Hiu used similar methods to calculate π and determine the area of a circle.
Of course, Archimedes, Liu Hui, and their contemporaries did not invent calculus. But it’s not difficult to see how this idea relates to integral calculus. In integral calculus, which is concerned with finding the areas beneath curves (among other things), the principal strategy is to divide these areas up into increasingly infinitesimal slices, find the areas of these slices, and then add them together to find the area of the whole.
Paradoxes of infinity
Another integral (ahem) part of calculus is the infinite series, which is a series of numbers that continues indefinitely. We saw a geometric version above in the method of exhaustion. Another spacial application of an infinite series is Zeno’s Paradox of Achilles and the tortoise, which goes something like this:
Achilles and a tortoise decide to race. Achilles gives the tortoise a head start of, say, 100 meters. In order to pass the tortoise, Achilles must close that 100 meter gap. By the time Achilles has closed it, the tortoise has moved some distance further, say, 10 meters. Achilles must now close this distance, during which time the tortoise will have moved even further. So how will Achilles ever catch the tortoise?
A similar paradox stated by Zeno, called Dichotomy, states that if a person, let’s call her Athena, wishes to walk one mile, she must first cover half a mile. To cover half a mile, Athena must first cover half that distance, i.e., a quarter mile. To cover a quarter of the distance, Athena must first cover half that distance, i.e., an eighth of a mile, and so on.
Achilles converges on victory
These may be paradoxes of thought, but they are not paradoxes in reality. Achilles will catch the tortoise, and Athena will reach her destination. The challenge is explaining the mathematical explanation for why this is so.
The key here is the idea of a convergent series. Strangely enough, it is possible to take the sum of an infinite series of numbers, but the series must be convergent. The term convergent here means that the sum of the series converges on a particular number.
With the example of the Dichotomy above, the distance Athena covers can be represented as ½ + ¼ + ⅛ + …. We know, intuitively, that the sum of these values converges on (sums to) 1, since that’s the entire distance she’ll cover.
Half (of half) of a ruler
Another way of thinking about a convergent series is to imagine a ruler that’s a foot long. This same ruler could be divided up into halves, ½ + ½ and still have the same length of 1 (1 = ½ + ½). One of those halves could be divided in half again (1 = ½ + ¼ + ¼). One of those quarters could be divided in half (1 = ½ + ¼ + ⅛ + ⅛). We could carry this process on forever and never change the length of the entire ruler.
We’ve shown that it’s possible to take an infinite number of things and add them together to get a non-infinite result. This is one of the foundational ideas of calculus, and the seeds were sown thousands of years before Newton and Leibniz.
Tangent lines pointing toward derivatives
Just as integral calculus is largely concerned with the areas beneath curves, differential calculus is focused on rate at which those curves change. One way to describe this rate of change is to draw straight line that just touches the curve. This is called a tangent line.
The tangent (red) of a curve (black).
There are different ways to describe how to draw such a tangent line. One way is to connect two dots which are infinitely close on the curve. Another (more practical) way is to draw a line that’s perpendicular to the curve at a given point. The tangent will be perpendicular to that line.
Mathematicians have been drawing tangents for thousands of years. They show up in Euclid’s Elements and Archimedes, for his part, demonstrated a method for finding the tangent line to a spiral.
Calculus fundamentals
One of the best parts about learning calculus is that once you move into integral calculus, you see that differentiating a function (finding the rate of change) can be thought of as the inverse of integrating a function (finding the area underneath the curve). This is no accident, and the Fundamental Theorem of Calculus shows how definite and integral calculus are two parts of the same thing.
One could be forgiven for concluding that if Leibniz and Newton are the indisputable fathers of calculus, then its fundamental theorem was what they created. But the Fundamental Theorem actually came earlier. James Gregory, the Scottish mathematician, published his limited proof of it in 1668. Later, Isaac Barrow published a more generalized and complete proof. James Gregory died at 36. And Barrow died at 46, but not before he passed the torch of calculus to his student, Isaac Newton.
Newton and Leibniz
There is now wide agreement that calculus was invented independently and contemporaneously by the Englishman Isaac Newton and by the German Gottfried Leibniz.
Isaac Newton and Gottfried Leibniz.
During their lives, however, their was no such agreement. Newton is believed to have developed the ideas first, but Leibniz was the first to publish. And an important part of the controversy was animosity between England and the European continent. In that sense, it wasn’t so much a debate of which man invented calculus, but to which countries it belonged.
Inventing calculus
So how could Barrow and Gregory have proved the Fundamental Theorem of Calculus if it hadn’t been invented yet? The key point here is that calculus is more than a theorem linking integrals and derivatives. If it were just that theorem, then it could be taught in a few days rather than over the course of several years. Calculus is an entire system, with methodology, symbolism, and relationships. So when we say that Leibniz and Newton “invented” calculus, what we mean is that they created these systems.
Beyond calculus
Both Newton and Leibniz made many other contributions besides the development of modern calculus. Newton is credited with discovering gravity and classical mechanics, pushing forward the study of optics, inventing a generalized binomial theorem, and much more besides.
Leibniz, for his part, helped develop formal logic, contributed to the theory of matrices determinants, developed the foundations of topology, and theorized on binary numerals and what we now call computer science. Indeed, his Wikipedia page lists no fewer than 26 “main interests,” from mathematics to ethics to sociology to poetry. In terms of calculus itself, it was Leibniz who gave it its name (from the latin for “small pebble”) and dominate symbolism.
Everyone else
In addition to Leibniz and Newton and their predecessors Gregory and Barrow, there were many other mathematicians involved in the development of calculus, both before and after Leibniz and Newton. A few prominent subjects, in more or less chronological order:
- Pierre de Fermat: Developed a means of calculating minima, maxima, and tangents.
- René Descartes: Developed analytical geometry a key part of the discovery of calculus.
- Johann and Jakob Bernoulli: Proposed problems eventually became part of the calculus of variations.
- Leonhard Euler: Elaborated on the calculus of variations.
- Joseph-Louis Lagrange: Further elaborated on the calculus of variations.
Onward
Calculus is no longer just the realm of academics and professional mathematicians. Whether or not you ever studied it, calculus has undoubtedly touched nearly every aspect of your life. It’s a central part of construction, electronics, finance, science, medicine, and on and on. And despite the fact that it took many millennia of human civilization to discover and develop, it’s now studied by millions of students the world over.
With that in mind, I’ll close with Maria Gaetana Agnesi, who is described by the Encyclopedia Britannica as “the first woman in the Western world to have achieved a reputation in mathematics.” Her magnum opus, Analytical Institutions, was a teaching text and the first book to address both differential and integral calculus. It was also the first mathematics book published by a woman.