This year I’m teaching math to 6th graders through 10th graders. As my kids get older, they tend to get better at math, which is not surprising. But I’m also finding that there’s another skill that my students are actually getting worse at as they get older: being wrong. My 6th graders are actually really good at being wrong, and when I tell them this they’re always keen to flex their burgeoning sarcasm muscles and say something to the effect of, “Thanks Mr. Alex, we really appreciate the compliment.”
What does it mean to be good at being wrong? Yesterday we were figuring out the fiftieth number in a sequence if we were given the sequence’s first three numbers. For one sequence in particular a student raised her hand and volunteered 202, then after a brief pause someone else volunteered 197. Even though neither of these answers was correct, we already had some disagreement. Something to talk about! Someone offered 252, and then finally another student offered 250. We then talked through the pattern underlying the sequence and found that the correct value for the fiftieth step was 252.
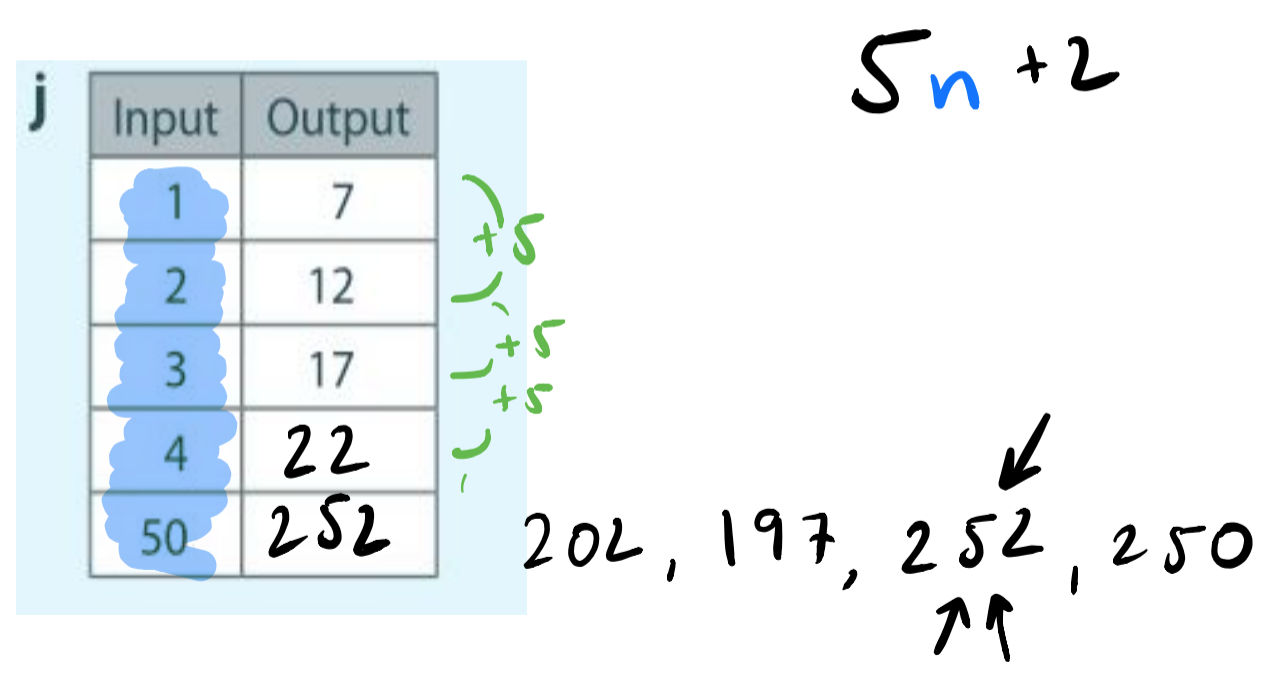The sequence in question.
Having come up with an explanation for the correct value, we then turned to the incorrect values. I asked the students who volunteered them to share their thinking. Following the Anna Karenina principle, each was wrong in its own way. And while they were wrong in interesting, illuminating ways (because of misunderstandings of the rules of multiplication, for example, or of how sequences worked), that’s not my point. My point is that the students who had come up with incorrect values still felt comfortable talking about them, explaining where they went wrong, and how their understanding had evolved. They didn’t see their incorrect answers as who they were as a person, whether they were “smart” or “dumb,” a “math person” or not. In short, they were good at being wrong.
I want my students to arrive at the correct answers using correct understanding. But it’s much harder to arrive at that destination if they’re terrified of taking a first step. And a big part of what makes that first step terrifying is that it might not be exactly or completely right. Now the question is how to preserve and foster this ability. More on that later.